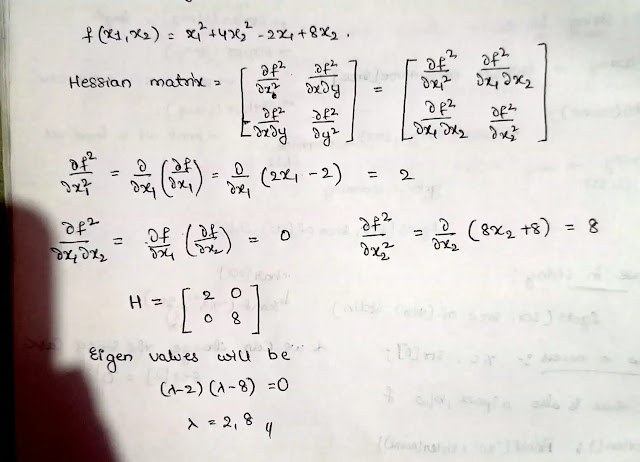NPTEL Data Science for Engineers Assignment 5 Answers 2023? In this article we will discuss about the answers for Week 4 assignment of Data science for Engineers. All these answers are make it as reference. I am confident in providing these answers. Then Come with us until the last of page to know more about week 5. 

Also Read:   Nptel Data Science Week 4 Assignment Answers 

About Nptel

NPTEL (National Programme on Technology Enhanced Learning) is an initiative by the Indian government that offers online courses and certification in various fields of engineering, science, technology, management, and humanities. It was established in 2003 by the Indian Institutes of Technology (IITs) and the Indian Institute of Science (IISc), with the aim of improving the quality of education in these fields.

NPTEL offers courses in various formats, including video lectures, online assignments, and online exams. The courses are developed and taught by faculty members from the IITs and IISc, and are designed to be accessible to learners from all over the world. NPTEL also offers certification for many of its courses, which can be earned by passing the online exam at the end of the course.

NPTEL courses are available for free, and learners can enroll in as many courses as they want. The program has gained a lot of popularity over the years, with over 700 courses and over 40 lakh registered learners as of 2021.

NPTEL Data Science for Engineers Assignment 5 Answers 2023 

Last Date: 01-03-2023

You can find the answers for Data Science for Engineers Assignment 5 Answers 2023 below

Q1. Which of the following statements is/are not TRUE with respect to the multivariate optimization?

I - The gradient of a function at a point is parallel to the contours

II - Gradient points in the direction of greatest increase of the function

III - Negative gradient points in the direction of the greatest decrease of the function

IV - Hessian is a non-symmetric matrix 

a.  I 

b.  II and III

c.  I and IV 

d.  III and IV

Answer: [ C ]

 

From the above Pic we can select Option 1, But we have to check option 4 also.

Hence, we can select Option 3.

Q2. The solution to an unconstrained optimization problem is always the same as the solution

       to the constrained one. 

a.  True

b.   False

Answer: [ B ] False 

You can also check this at Week 5 video 1 at 05:59.

Q3. Gradient based algorithm methods compute ____

a. only step length at each iteration

b. both direction and step length at each iteration 

c. only direction at each iteration

d. None of the above

Answer: [ B ] both direction and step length at each iteration 

Q4. For an unconstrained multivariate optimization given f(x¯), the necessary second order 

       condition for x¯∗ to be the minimizer of f(x) is 

a. ∇2f(x¯∗) must be negative definite.

b. ∇2f(x¯∗) must be positive definite.

c. ∇f(x¯∗) = 0

d. f "( x¯∗) > 0

Answer: [ B ]  ∇2f(x¯∗) must be postive definite.

Use the following information to answer Q5, 6, 7 and 8

   minx1,x2∈R f(x1,x2)=x1^ 2 +4x2^2−2x1+8x2.

Q5. Which among the following is the stationary point for f(x1,x2)?

a. ( 0, 0 )

b. ( 1, -1 )

c. ( -1, -1 )

d. ( -1, 1 )

Answer: [ B ]  (1, -1) 

Q6. Find the eigen values corresponding to Hessian matrix of f.  

a.  1,-1 

b. 1, 1

c. 2, 8 

d. 0, 8 

Answer: [ C ]  2,8

Q7. Find the minimum value of f. 

a.  0

b. -5 

c. -1 

d.  1

Answer: [ B ]  -5 

Q8.  What is the minimum value of f(x1,x2) subject to the constraint x1+2x2=7?

a. -5 

b.  -1 

c.  27 

d.  0 

Answer: [ C ] 27  

Q9. Find the maximum value of f(x,y)=49−x^2−y^2 subject to the constraint x+3y=10.

a. 49

b. 46

c. 59

d. 39

Answer: [ D ] 39

Q10. 

Answer: [ A ]

Because for lagranges, general formula is f(x,y, . . . ) = f(x,y) + u*g(x,y) + u*g(x,y) + . . . . 

Also Read:   Nptel Data Science Week 4 Assignment Answers 

Conclusion:

I Request everyone to revisit the website on/before to last date for any re-verification of answers.

If you have any queries, contact us. I am very thankful to answer you.

NOTE: I'm answering these questions to the best of my knowledge.